不动点法用于求解一元方程。它的基本原理是这样的:
例如我有一个方程 ,那么将这个方程等价变形为
。
其实在这里,可以画出两个函数的图像,图像的交点就是答案。
说好的迭代呢………………
- 任意取一个 x
- 代入
中
- 求得一个
- 令
,转第二步。
没错就是这么简单。
代码
拿 Matlab 写代码好了……Python 的 plotlib 有时候真心 bug,图片死都出不来。怪我喽?
我们要求方程 的唯一实根。
clear all;
close all;
clc;
d = 1e-6;
x=[0:0.1:3];
y=(20-x.^3)/10;
% y=nthroot(20-10*x,3);
% y=-10./x+20./x./x;
plot(x,y)
hold on
plot(x,x)
hold on
a = 2;
b = (20-a.^3)/10;
% b = (20-10*a)^(1/3)
% b = -10/a+20/a/a;
while abs(a - b) > d
ta=a;
a = b;
b = (20-a.^3)/10
% b = nthroot(20-10*a,3)
% b=-10/a+20/a/a
plot([ta,a,a],[a,a,b])
% plot(a,b,'x')
end
title('点变化轨迹')
disp('计算结果:')
fprintf('%6f\n',b)
% w = [1 0 10 -20];
% x = [-10:0.01:10];
% y = polyval(w,x);
% plot(x,y)
实际上,对于给定的方程,第一步的 “转化” 有很多种形式,可以是 ,可以是
,也可以是
。真的不是因为爱才选了第一种形式…… 而是因为,选择其他两种形式非常难得到结果。把图画出来,看一下点的轨迹就知道了(不收敛 / 很难收敛)。
还有一个坑是,Matlab 不能做负数开三次根号。问: 等于多少?你看看在 Matlab 下面算
(-1)^(1/3) 给出的复数是多少?等等,为啥是复数?!
效果图
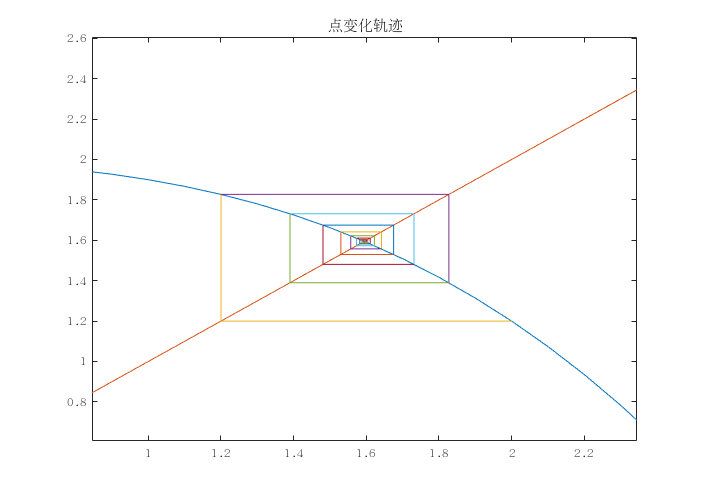
嗯最终收敛了!
发表回复