做一个简单的梯度下降

为什么要梯度下降？

梯度是上升最快的方向。那么，沿着梯度的反方向，一定是下降最快的方向。

用梯度下降可以比较快地找到函数的某个极值。

怎么做？

1. 指定一个步长 alpha。
2. 随便找一个点。
3. 求函数在这点的梯度。
4. 沿着梯度的方向走一个 alpha 步长，当作新点。
5. 重复前面两步，直到收敛。

有什么需要注意的事儿呢？

• “同步更新”。也就是说，如果在一个 n 维空间做梯度下降，那么一定是有 n 个参数。我们必须同时求这 n 个参数的梯度，之后再 “走一步”。不能先求第一个参数的梯度，走一小步，再求第二个参数的梯度，再走一小步……

给个例子？

我们求恶意函数（我也不知道为啥叫这个名字） 的极值

clear all;
close all;
clc;

x1_start=10;
x2_start=-20;
alpha = 0.01;

tmax=max(abs(x1_start),abs(x2_start))
[x1,x2] = meshgrid(-tmax:0.2:tmax);
y= (1-x1.^2).^2+(x1-x2).^4;
mesh(x1,x2,y);
hold on

x1 = x1_start;
x2 = x2_start;
alpha2=alpha*2;
while true
    f = (1-x1^2)^2+(x1-x2)^4;
    plot3(x1,x2,f,'.')
    px1 = 4*x1*(x1^2 - 1) + 4*(x1 - x2)^3;
    px2 = -4*(x1 - x2)^3;
    x1=x1-alpha*x1;
    x2=x2-alpha*x2;

    if abs(px1) < alpha2 && abs(px2)<alpha2
        break
    end
end;
hold off
    

结果

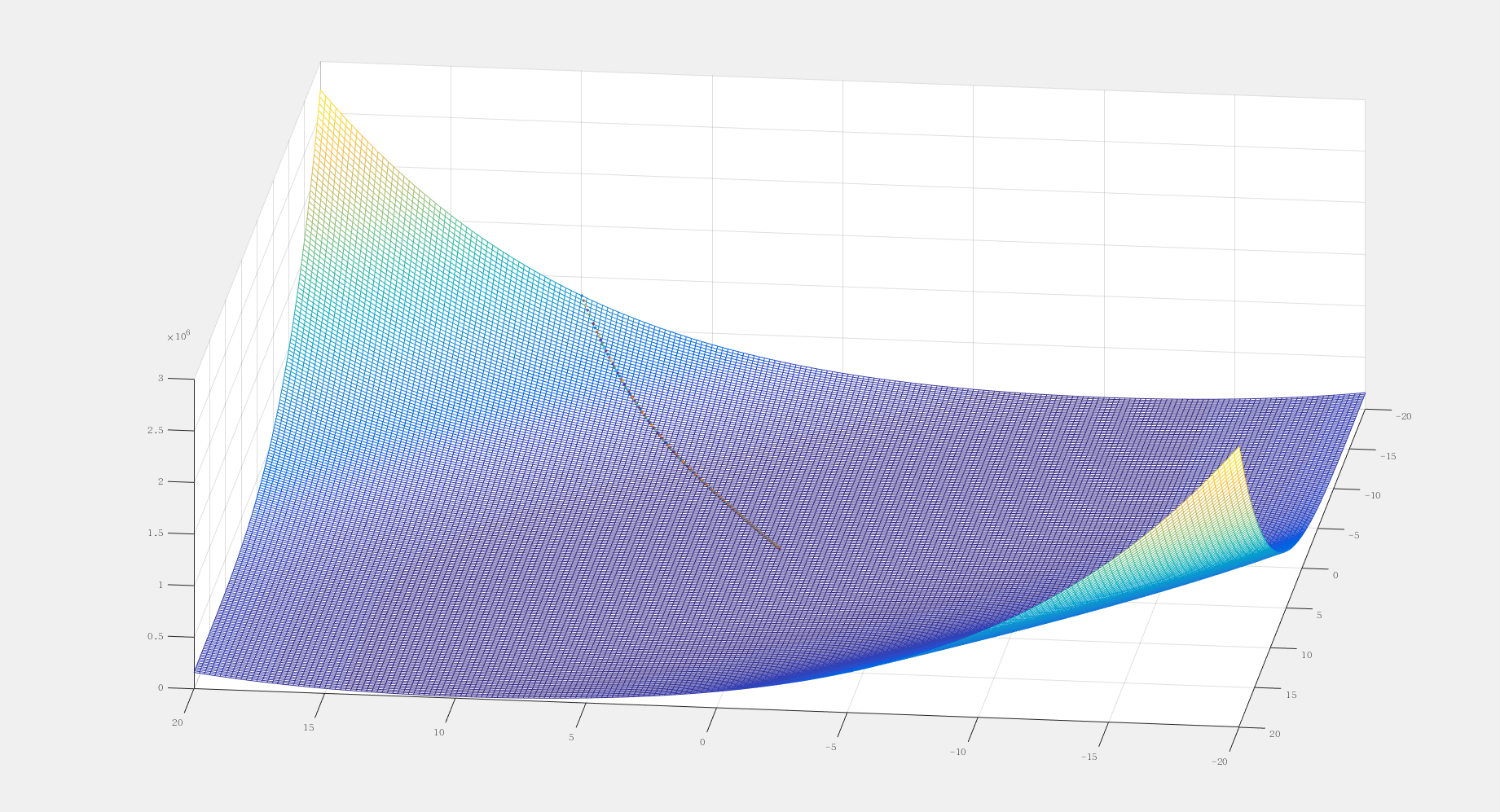
注意图中的那个黑线，就是梯度下降的轨迹。这个函数的梯度下降曲线比较 “好”，几乎走了一条直线。正常情况下应该是走一个“之” 字形的路径。

参考

• https://en.wikipedia.org/wiki/Gradient_descent