数据降维用的。
原理…… 原理我还没太懂…… 那么多的 PPT 得一点一点理解……
直接放代码。
lanczos.m 文件:
function T = lanczos(A,v,k)
% LANCZOS A simple implementation of the Lanczos process using matrixop
%
% T = lanczos(A,v,k) returns the tridiagonal matrix T of coefficients for
% the Lanczos process after k steps, starting with the vector v. The
% matrix A must be a matrixop class or a Matlab matrix. The operator
% matrix A must be symmetric.
%
% See Golub and van Loan, Matrix Computations, 3rd Edition for more
% information.
% initialization
v = v./norm(v);
r = v;
b1 = 1;
v1 = 0;
T = zeros(k,k);
% computation
i = 0;
while (i < k-1)
v = r/b1;
i = i+1;
p = A*v;
T(i,i) = v'*p;
r = p - T(i,i)*v - b1*v1;
b1 = norm(r);
T(i,i+1) = b1;
v1 = v;
end
% finish the final step
v = r/b1;
i = i+1;
p = A*v;
T(i,i) = v'*p;
% set the lower diagonal
T = T + diag(diag(T,1),-1);
main.m 文件:
clear all;
close all;
clc;
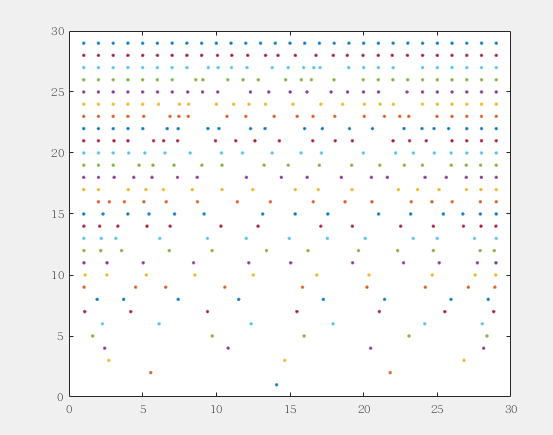
n = 29;
e = ones(n,1);
A=diag([1:1:n]);
for ki = 1:1:n
t=eig(lanczos(A,rand(n,1),ki));
plot(t,ones(ki,1)*ki,'b.')
hold on
end
效果截图
参考资料
- Scientific Computing: An Introductory Survey, Chapter 4 – Computing Eigenvalues and Eigenvectors – Power Iteration and Values – Example: Lancoz Iteration
- 上述教材的 PPT,Page 69
发表回复