本文是对文章《Normalized cuts and image segmentation》的一个简单实现。各种错误请指正!
简介
这个算法的核心思想是,将一个传统意义上的 “图片” 转变为数学上的 “图”(由 A.jpg 转变为 ),通过对图中边权的计算,将图像分割问题转变为求矩阵特征值问题。拿到矩阵特征值,问题就解决了。
一步一步来
一些定义
w:两个点之间连一条边,这个边的权重。对于图片来说,可以是像素灰度差之类的东西;对于数学中的图来说,可以是两点之间的距离 / 欧式距离等东西。
:两个集合之间的边权的总和。如果需要将这两个集合 “割开”,那么需要消耗这么多权重。
:相当于做了个归一化吧。assoc 就相当于 cut。
W:由 w 组成的大矩阵。
d:点 i 发出的边的权值总和。
D:将 d 向量变成一个对角阵。
其他定义不太重要,貌似都是在玩公式时会用到的。
如何分割?
给一个由 1 和 -1 组成的向量:如果第 i 个点属于 A,那么 ,否则
。所以
可以把
x=1 的元素找出来, 可以把
x=-1 的元素找出来。
那么,可以把 Ncut 的式子转变成
$$ Ncut(A,B)=\frac{\sum_{x_{i}>0,x_{j}<0}{w_{i,j}}}{\sum_{x>0}{d_{i}}}+\frac{\sum_{x_{i}<0,x_{j}>0}{w_{i,j}}}{\sum_{x<0}{d_{i}}} $$
然后再来定义一个
$$ k=\frac{\sum_{x_i>0}{d_i}}{\sum{d_i}}=\frac{(1+X)^TDX^T}{21^TD1}=\frac{(1+X)^TD1}{21^TD1} $$
这时,为了简化计算,我们可以算一下这个式子:
$$4Ncut(x)=\frac{(1+x)^T(D-W)(1+x)}{k1^TD1}+\frac{(1-x)^T(D-W)(1-x)}{(1-k)1^TD1}$$
(为什么是 4 倍呢?因为 和
下面的 2 都跑到哪里去了呢?)
这个式子很巧妙,反正我是想不出来这样的式子。把这个式子通分一下,就可以得到 这个结果了。
为了写着方(Tou)便(Lan),我们做以下定义:
:这个东西其实是
。
:这东西其实是个 0。
:这东西其实也是个 0。
:这东西其实是
D 的 sum,或者说是 W 的 sum。
下面的事情就是如何证明 公式 4 是正确的了。“显而易见”,但是由于我数学太渣,证明了好长时间…… 都是泪
下面是一些推导步骤:
定义 和
,求证
,即证
。
$$ 1^TD1+x^TD1=\frac{k}{1-k}(1^TD1-x^TD1) $$
$$ (1-k)(1^TD1+x^TD1)=k1^TD1-kx^TD1 $$
$$ 1^TD1+x^TD1-k1^TD1-kx^TD1=k1^TD1-kx^TD1 $$
$$ 1^TD1+x^TD1=(1+x)^TD1 $$
所以公式 4 是正确的。(好了作业完成!囧……)
然后整个问题就转变成了公式 5,是一个瑞利商问题,继而转变成特征值问题。原谅我这部分实在转不过来弯…… 剧情发展太快了。
在获得特征值和特征向量之后,对特征值进行排序,舍弃掉最小的特征值和其对应的特征向量。之后,每个特征值可以对应一个特征向量,把特征向量看作上面的 x,进行掩模,就得到了分割后的图像。
代码
代码分为几个部分: 第一部分,Ncut 的核心代码。第二部分,生成随机点,为点分割做数据源。第三部分,点分割。第四部分,图像分割。
其中,第三和第四部分是 Demo。
solve_ncuts.py
import numpy as np
def n_cuts(W, regularization):
if regularization is True:
# Regularization
offset = 5e-1
D = np.sum(np.abs(W), axis=1) + offset * 2
W += np.diag(0.5 * (D - np.sum(W, axis=1)) + offset)
else:
# Without Regularization
D = np.sum(np.abs(W), axis=1)
# Three ways to calculate T
# T = np.linalg.inv(D ** (1 / 2))
T = np.power(D, -1 / 2)
# T = 1. / np.sqrt(D)
# Change D to a Diagonal one
D = np.diag(D)
# Calculate eigenvalues and eigenvectors
# eigenvalues, eigenvectors = np.linalg.eig(T * (D - W) * T)
(_, eigenvalues, eigenvectors) = np.linalg.svd(T * (D - W) * T)
return eigenvalues, eigenvectors
这里 T 的计算(公式 13)有好几种方法。
还有一个比较神奇的地方:eig 和 svd。eig 是求矩阵的特征值和特征向量,速度比较慢(大约为 $O(n^3)$),svd 是奇异值分解,速度比较快。干的事情 “几乎相同”(By 同学),但是实际测试中发现,使用 eig 效果非常不好,完全不能达到论文中的效果,而使用 svd 效果就不错。论文中附带的代码也是使用的 svd。
gen_data_points.py
import numpy as np
def make_data_fixed_points():
return np.array([(1, 1), (1, 2), (2, 1), (2, 2),
(1, 3), (1, 4), (2, 3), (2, 4),
(3, 1), (3, 2), (4, 1), (4, 2),
(10, 1), (10, 2), (1, 10), (2, 10)])
def make_data_two_part():
sigma_h = 2
sigma_v = 10
s_v = 10
s_h = 30
a = np.array([sigma_h * np.random.random(40),
sigma_v * np.random.random(40)])
b = np.array([sigma_h * np.random.random(50),
sigma_v * np.random.random(50)]) + \
np.array([[s_h], [s_v]]) * np.ones((1, 50))
return np.hstack((a, b)).transpose()
def make_data_three_part():
radius = 15
size_cluster = [80, 20, 20]
raw_data = np.random.randn(2, sum(size_cluster))
tmp = np.random.randn(2, size_cluster[0]) - 0.5
idt = tmp[1].argsort()
r_noise = 4
raw_data2 = np.array([tmp[0, idt] * r_noise,
tmp[1, idt] * 2])
data1 = np.array([(radius - raw_data2[0, 0:size_cluster[0]]) * np.cos(np.pi * raw_data2[1, 0:size_cluster[0]]),
(radius - raw_data2[0, 0:size_cluster[0]]) * np.sin(np.pi * raw_data2[1, 0:size_cluster[0]])])
center = np.array([0, 0])
sig = np.array([1, 2])
scb = size_cluster[0] + 1
scb_next = scb + size_cluster[1] - 1
data2 = np.array([center[0] + sig[0] * raw_data[0, scb:scb_next],
center[1] + sig[1] * raw_data[1, scb:scb_next]])
center = np.array([radius + 20, 0])
sig = np.array([1, 1])
scb = scb_next + 1
scb_next = scb + size_cluster[2] - 1
data3 = np.array([center[0] + sig[0] * raw_data[0, scb:scb_next],
center[1] + sig[1] * raw_data[1, scb:scb_next]])
return np.hstack((data1, data2, data3)).transpose()
def make_points(points_type):
data = {1: make_data_fixed_points,
2: make_data_two_part,
3: make_data_three_part}
return data[points_type]()
第一部分是我自己做测试用的 16 个点,第二和第三部分是论文中的点生成办法,看着比较漂亮。
demo_points.py
import numpy as np
import matplotlib.pyplot as plt
from gen_data_points import make_points
from solve_ncuts import n_cuts
def compute_connection(points):
n_items = len(points)
distance = np.zeros((n_items, n_items), dtype=np.float)
for which in range(n_items):
distance[which, :] = np.sqrt(
np.power(points[:, 0] - points[which, 0], 2) +
np.power(points[:, 1] - points[which, 1], 2)
)
scale_sig = np.max(distance)
W = np.exp(-np.power(distance / scale_sig, 2))
return W
def segment_and_show(points, eigenvalues, eigenvectors):
abs_eigenvalues = np.abs(eigenvalues)
print(abs_eigenvalues[abs_eigenvalues.argsort()])
# Only show 4 graphs
for pos in abs_eigenvalues.argsort()[1:min(5, len(abs_eigenvalues))]:
eigenvector = eigenvectors[pos] > 0
points_a = points[eigenvector]
points_b = points[~eigenvector]
# Adjust image form
plt.figure()
plt.grid(True)
plt.axis('equal')
# Show data
plt.plot(points_a[:, 0], points_a[:, 1], 'ro')
plt.plot(points_b[:, 0], points_b[:, 1], 'bo')
plt.show(block=False)
print("Collection A: {}".format(len(points_a)))
print("Collection B: {}".format(len(points_b)))
print("Item Select: {}".format(pos))
print("Value: {}".format(abs_eigenvalues[pos]))
print("=" * 10)
if __name__ == '__main__':
# 1: Fixed 16 points
# 2: Two parts
# 3: Three parts
points = make_points(3)
W = compute_connection(points)
(eigenvalues, eigenvectors) = n_cuts(W, regularization=False)
segment_and_show(points, eigenvalues, eigenvectors)
input("Press ENTER to continue...")
plt.show(block=False) 这一句话可以使显示 figure 的时候不被阻塞,否则只能关掉 figure 才会进行下一步。
demo_picture.py
这个代码和上面分割点的代码差不多。
import numpy as np
import skimage
import skimage.io
import skimage.color
import matplotlib.pyplot as plt
from solve_ncuts import n_cuts
def read_image(filename):
img = skimage.io.imread(filename)
if 3 == img.ndim:
return skimage.img_as_ubyte(skimage.color.rgb2gray(rgb=img))
else:
return skimage.img_as_ubyte(img)
def compute_connection(image):
image_flat = image.ravel()
n_items = len(image_flat)
distance = np.zeros((n_items, n_items), dtype=np.float)
for which in range(n_items):
distance[which, :] = np.abs(image_flat - image_flat[which])
scale_sig = np.max(distance)
W = np.exp(-np.power(distance / scale_sig, 2))
return W
def segment_and_show(image, eigenvalues, eigenvectors):
image_shape = image.shape
abs_eigenvalues = np.abs(eigenvalues)
print(abs_eigenvalues[abs_eigenvalues.argsort()])
# Only show 4 graphs
ith = 0
for pos in abs_eigenvalues.argsort()[1:min(5, len(abs_eigenvalues))]:
eigenvector = eigenvectors[pos] > 0
cut_area = image * eigenvector.reshape(image_shape)
# skimage.io.imshow(cut_area)
skimage.io.imsave('result/result_{}.jpg'.format(ith), cut_area)
ith += 1
if __name__ == '__main__':
image = read_image('data/Terracotta_small.jpg')
W = compute_connection(image)
(eigenvalues, eigenvectors) = n_cuts(W, regularization=False)
segment_and_show(image, eigenvalues, eigenvectors)
input("Press ENTER to continue...")
在这里发现一个 bug:如果使用了 skimage,那么就不能显示 figure 了(figure 窗口跳不出来)。我也不知道问题出在哪里。所以改成输出图片进行观察了。
在论文中提到了如何把图像转变成图。最最简单和原始的方法就如这里代码所写,每个像素当作一个点。OK 速度慢死……
效果
分割点的效果
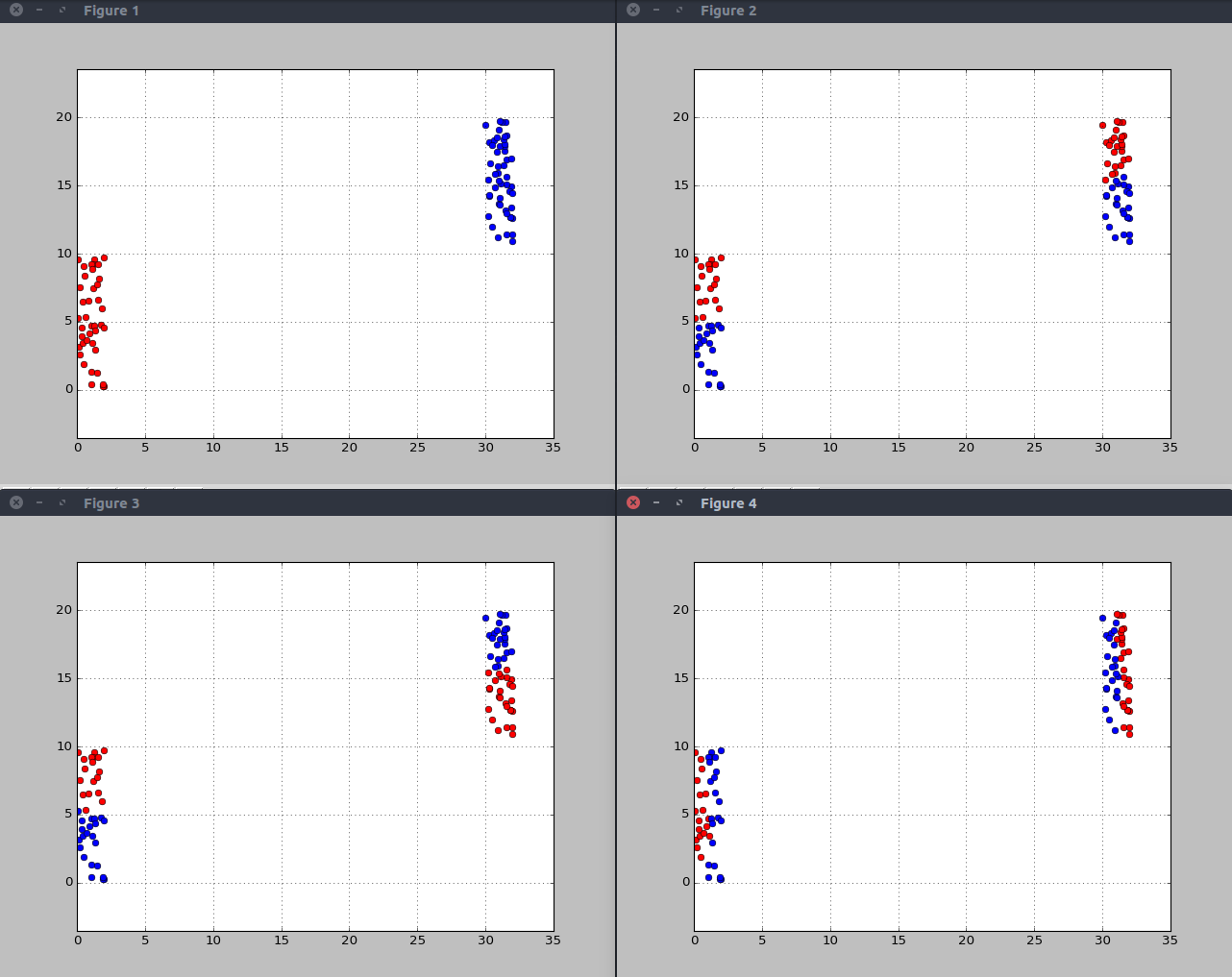
第一个效果还是比较好的吧,后面的都是什么鬼?
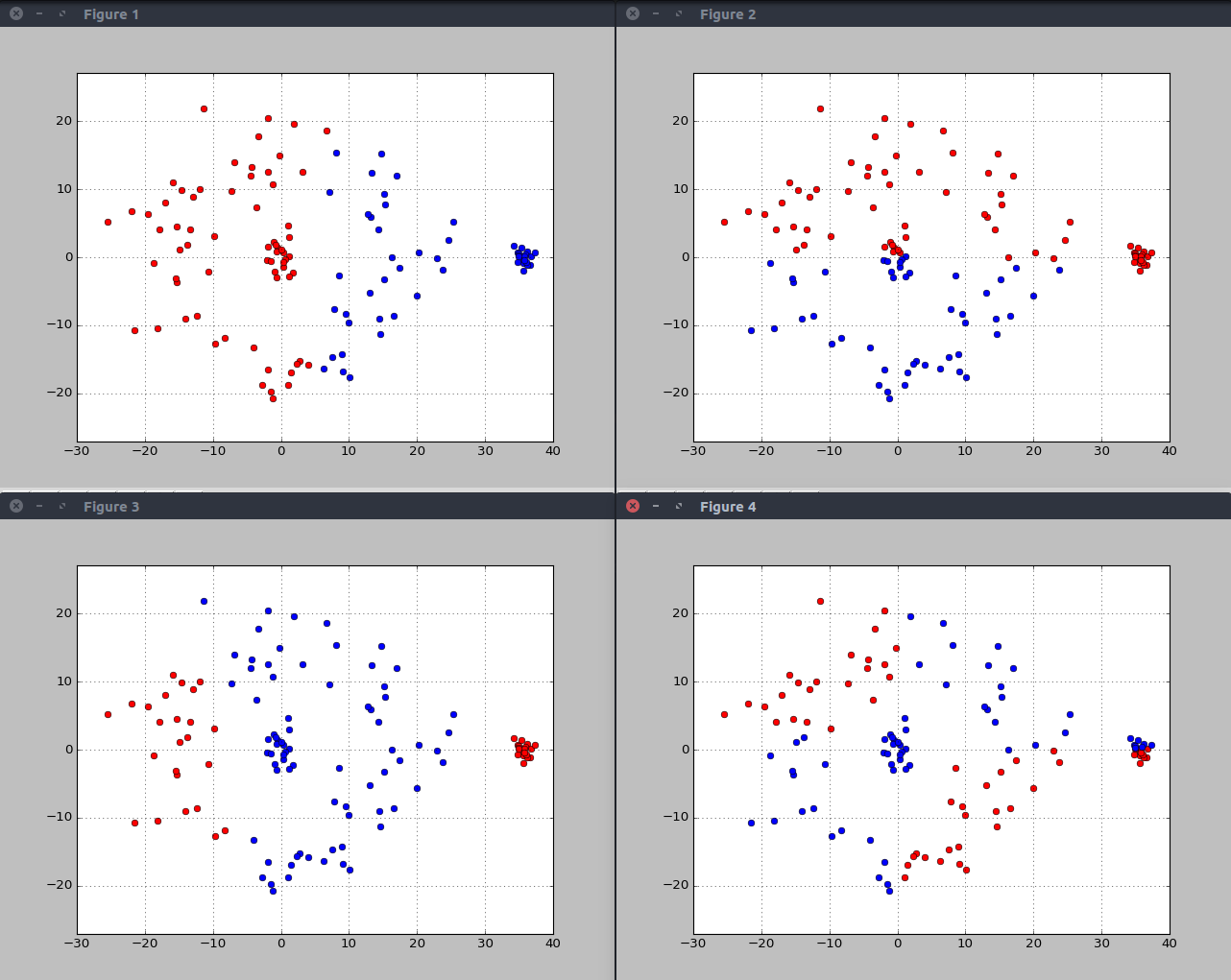
这效果是什么鬼?
分割图片效果

总结
老师说:“不要用!”
参考资料
- Shi J, Malik J. Normalized cuts and image segmentation[J]. IEEE Transactions on pattern analysis and machine intelligence, 2000, 22(8): 888-905.
- MATLAB Normalized Cuts Segmentation Code, https://www.cis.upenn.edu/~jshi/software/
发表回复