[LeetCode] Container With Most Water

题意

在一个 1～N 的数轴上，每个点向上画一个长度为 ai 的线段。找出两个线段 ai 和 aj，使 min(ai,aj)*(j-i) 这个矩形面积最大。

题解

第一次尝试

最容易想到的是二重循环。时间复杂度是 O(N^2)。数据量到 1000 的时候就过不去了。

如果用 C 的话可能还能更快一点，但是 Python 慢啊！

代码

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        len_height = len(height)
        ans = 0
        for i in range(len_height - 1):
            if not 0 == height[i]:
                for j in range(i, len_height):
                    ans = max(ans, min(height[i], height[j]) * (j - i))
        return ans

结果

Status: Time Limit Exceeded

第二次尝试

那就优化一下？

我们可以少做一些循环的：

1. 如果高度为 0，还用考虑么？
2. 在已经知道一个 ans 的情况下，外层循环枚举到 i，那么内层循环可以不从 i+1 开始枚举，而要从 i+ans/height[i] 开始枚举。

有人说加了以上条件就可以 AC 了。我想说，您是 C++/Java 吧？我大 Python 慢啊！

代码

class Solution(object):
    def maxArea(self, height):
        len_height = len(height)
        ans = 0
        for i in range(len_height - 1):
            if not 0 == height[i]:
                for j in range(i + (ans // height[i]), len_height):
                    ans = max(ans, min(height[i], height[j]) * (j - i))
        return ans

结果

Status: Time Limit Exceeded

第三次尝试

这个方法就比较牛了，时间是 O(n) 的。

我们设置两个指针 i 和 j，分别指向头部和尾部。

我们都知道一个名词叫做 “短板效应”：一个木桶能装的水的量是由最短的板子来决定的（你都不能把桶斜着放嘛！纯属鸡汤）。也就是说，我们需要尽可能地不要短板。

那么好，现在假设 heigh[i] 是短板。为了抛弃短板（如果 i 不动，那么能得到的最大面积就是 height[i]*(j-i) 了），需要 i 继续向后搜索，一边搜索一边计算面积。同样，如果 height[j] 是短板，那么需要 j 继续向前搜索。

有点贪心的意思哈。

官方给的解释图如下：

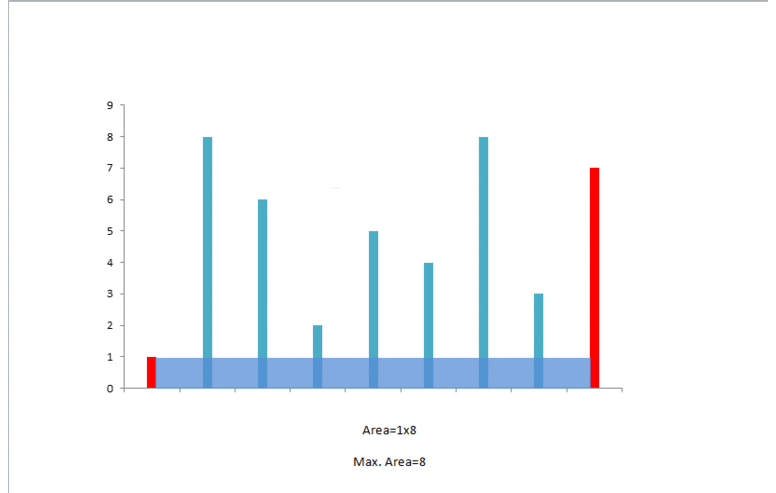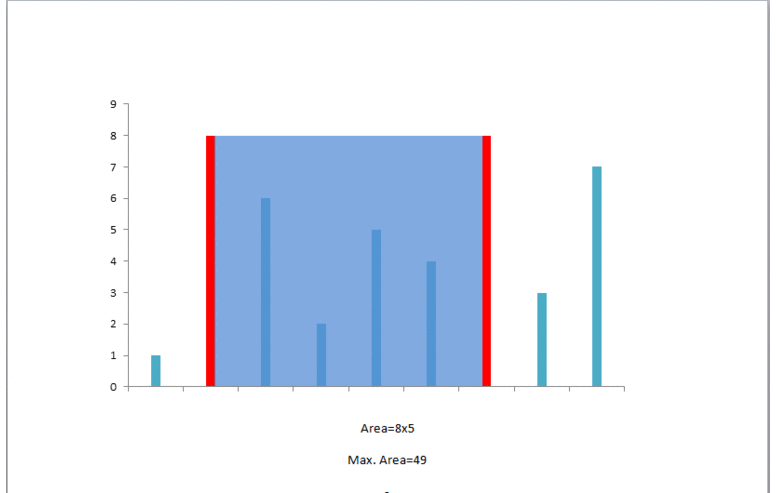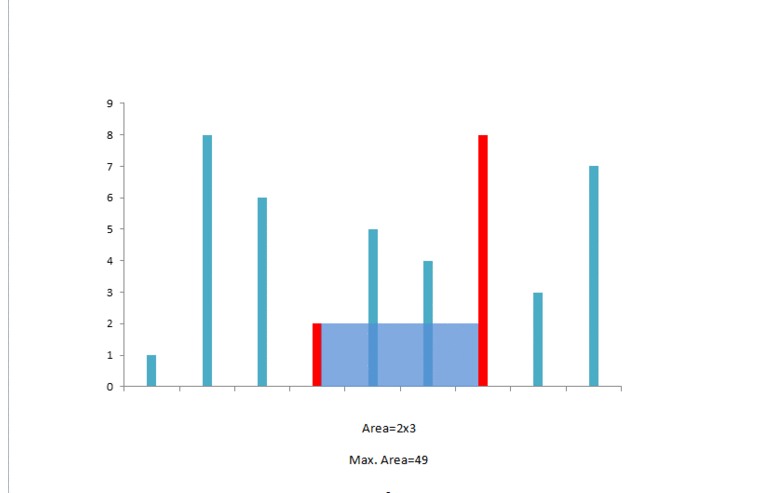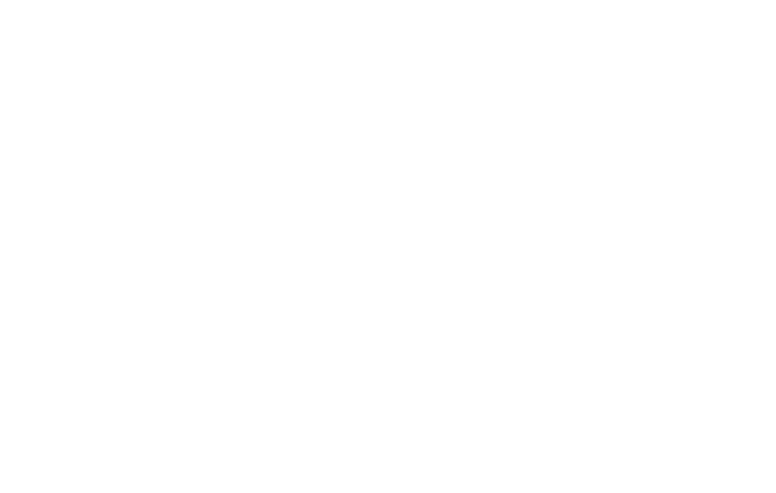
代码

class Solution(object):
    def maxArea(self, height):
        i = 0
        j = len(height) - 1
        ans = 0
        while i != j:
            ans = max(ans, min(height[i], height[j]) * (j - i))
            if height[i] < height[j]:
                i += 1
            else:
                j -= 1
        return ans

结果

45 / 45 test cases passed.
Status: Accepted
Runtime: 96 ms
Your runtime beats 38.81% of pythonsubmissions.

其他

想法很奇妙。但是为什么不是从里面向外扩张呢？排序有用没有？

桩程序

if __name__ == '__main__':

    cases = [
        {'height': [1, 1], 'ans': 1},
    ]
    for item in cases:
        ans = (Solution()).maxArea(height=item['height'])
        print(str(ans == item['ans']) + "\t=>" + str(ans) + ":" + str(item['ans']))